DDD Aggregates: Processes, State Machines and Transducers
An introduction to designing the Domain-Driven Design Aggregate pattern via first principles from automata theory

Photo by Michael Dziedzic on Unsplash
This blog post is the first one in a series of three posts in which we try to derive a mathematical model for process-oriented Domain-Driven Design (DDD) Aggregates.
The need for process-oriented models
In order to understand this need we need to dive into complex systems theory. Don’t worry, we will not dive deep!
Not surprisingly software is not an isolated artifact. It must be embedded into the socio-technical context of the people that use and produce it, paired with the constant interactions of the environment. What we need to know is how complex systems show the behaviors that we, as system designers, try to capture in useful abstractions.
Organizations are dynamic, hierarchically structured entities. Such dynamism is reflected in the emergence of significant events at every organizational level.
We will call these patterns of events processes. These processes emerge in systems to achieve something, be it selling books online or providing restaurants with seat reservations. A large research topic termed process theories is trying to understand how patterns of events lead to positive outcomes. Ultimately they are “stories about what happened and who did what when — that is, events, activities, and choices ordered over time” [Langley, A. 1999. Strategies for theorizing from process data].
The rise of collaborative temporal modelling
Over the past years new practices to capture these processes emerged. Event Storming, Story Mapping or Domain Story Telling are all examples of approaches to recognize that understanding the repeating patterns of events can give us a great leverage in designing working solutions. These results regularly have a much larger overlap with the organizational reality than traditional static modelling techniques.
Temporal modelling also had an effect on the tactical design choices that experienced DDD practitioners make when working with Aggregates. Aggregates are then defined as a combination of Commands (stimuli from the environment), Behaviors (reactions to incoming stimuli that can change the system’s response mechanisms) and Events (system signals in response to changes in system state). The “Event Sourcing” pattern for example builds on these fundamental design choices to make the time-ordered — hence “temporal” — patterns of events the central element of its design.
If we can define some Aggregates by time-ordered series of events, then it follows that these Aggregates are also processes.
Rediscovering Finite-State Machines
Modelling processes is nothing new in computing. And automata theory seems especially interesting:
A Finite-State Machine (FSM) formulation is used to describe the processes during which information or tasks move from one state to another for action, according to a set of rules. The states consists of the smallest amount of information that together with the knowledge of the input can determine the output.
The terms Automaton and Machine are used interchangeably, so when we talk about FSA, we also mean FSM.
Translated into our process terminology, FSMs process a stream of system stimuli (Commands), enforcing invariants and changing the system state (Behaviors).
The following figure (Fig. 2) shows how the temporal nature of FSMs is driven by the time-ordered and unidirectional stream of Commands.
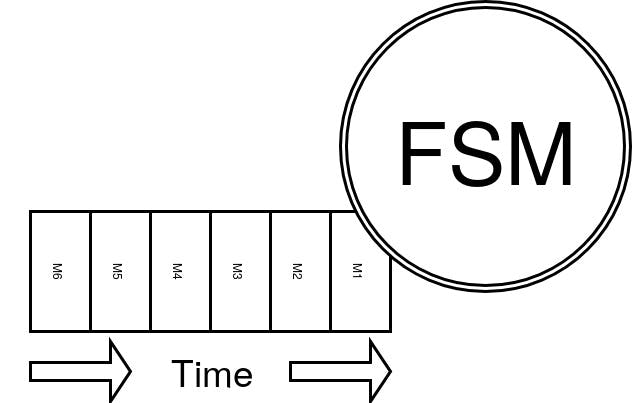
Since we want to derive a mathematical model, let’s look at the definition of an Finite-State Machine using our previously derived process terminology. An FSM Α is a 5-tuple
\[ A = \Big(S, C, \delta\colon S \times C \to S, S_0\colon S_0 \in S, F\colon F \subset S \Big) \]
where:
- S is a non-empty, finite set of states
- C is the Command language, a non-empty, finite set of Commands
- δ is the set of Behaviors — a relation between a state and Command to a state
- S₀ is the initial state where S₀ is an element of S
- F is the non-empty, finite set of final states where F is a subset of S
Given this definition, we will need to derive the command and state alphabets from the domain experts’ knowledge and then connect the dots via our Behavior functions.
The universe is a messy place
We love to look for deterministic solutions to problems that are complex and thus non-deterministic by nature. DDD as a modelling approach embraces unexpected behaviors of systems — which is one of the major reasons why I believe applying DDD thinking to complex problems is almost always a good choice. This means that responses to system stimuli are often different depending on the current situation. Imagine yourself as a call-center agent that is suddenly advised to re-route calls for specific topics to supervisors. The world is just not predictable. Non-deterministic Finite-State Auatomata (NDFA)
In order to deal with this messy world automata theory offers two distinct types of FSAs that can express these differences — Non-Deterministic (NDFA) and Deterministic (DFA) FSAs. Differences between DFA and NDFAs are subtle. While DFAs have exactly one transition for each state and command pair, NDFAs can have multiple, or even none. Mathematically, they are both equivalent. You can always transform a DFA into an NDFA and back again.
But they do differ between the amount of complexity required to represent them. An NDFA with n states can be transformed into a DFA with up to 2ⁿ states. For a decently complicated NDFA of 10 states we would need up to 1024 states in a DFA to represent it!
When using NDFAs you trade determinism for simplicity!
Where are the Events?
If we recollect the definition of the FSA — which was defined by the Command and state languages paired with the Behaviors — one might recognize that there is currently no way to signal anything back to the systems. So, where are the events?
It seems like a plain NDFA is not enough to represent our processes. Can automata theory provide another concept that we can use in this case?
Spoiler, yes it can!
Introducing Finite-State Transducers (FSTs)
Let’s compare the following schematic diagram of an FST (Fig. 4) with the previous one of an FSM (Fig. 2) and see if we can spot a difference:
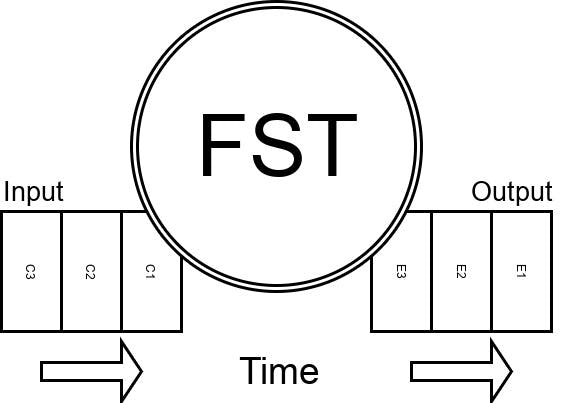
We now have an actual output of Events that correspond to the states and Commands that were fed in. Exactly what we need to send our signals out into the world to wreak havoc! Again, let’s have a look at the formal definition of an Finite-State Transducer. It is a 7-tuple
\[ A = \Big(S, C, E, \delta\colon S \times C \to S, \omega\colon S \times C \to E, S_0\colon S_0 \subset S, F\colon F \subset S \Big) \]
where:
- S is a non-empty, finite set of states
- C is the Command language, a non-empty, finite set of Commands
- E is the Event language, a non-empty, finite set of Events
- δ is the set of Behaviors — a relation of a state and Command pair to a state of form δ : S x C→ S
- ω is the output relation of a state and Command pair to an Event of form ω : S x C → E
- S₀ is the non-empty, finite set of initial states where S₀ ⊂ S (S₀ is a subset of S)
- F is the non-empty, finite set of final states where F ⊂ S (F is a subset of S)
Now that we have Commands, Behaviors and Events we can model our processes as non-deterministic FSTs. Let’s get to action and use the math in an example scenario!
A short excursion on the output relation ω (omega)
I quickly want to mention that automata theory differs between two major types of transducers — the Moore and Mealy types.
They are only different in the form of their output relation ω. Our transducer definition above is a Mealy Transducer, because its output relation ω depends on the state and Command as inputs, while a Moore Transducer's output relation would only depend on the state, and not the Command.
- Moore form: ω : S → E (Event generation depends only on state)
- Mealy form: ω : S x C → E (Event generation depends on Commands and state combined)
Example: Designing a User Registration Process
Let’s assume we have had a great Event Storming session and are now trying to apply the math to the crunched knowledge of a specific problem — a User Registration process. We have to define the Commands, States, Behaviors and the Events that should be written to the output in response to a specific Behavior. Since we have chosen Event Storming as our collaboration method of choice we'll start with the Events.
Speaking the Event language!
We start with building our Event language.
Confirmation was sent
After having started the registration we want to make sure that the customer really has access to the provided email address, hence we send out a confirmation via email with a confirmation link.
Confirmation resent
When the confirmation has expired we want to enable our customers to easily resend the confirmation, maybe the previous mail was caught by a spam filter.
Account was confirmed
When the confirmation was completed by the customer we say that the account is now confirmed.
Account was deleted through a GDPR request
We are bound by European laws to delete all personal data.
It follows that:
\[ E = \{\small{ConfirmationSent},\small{ConfirmationResent},\small{AccountConfirmed},\small{AccountDeleted}\} \]
Thou Command shall be my duty!
We have designed the following Commands analogous to our Events:
- Start registration
- Confirm account
- Resend confirmation
- Fulfill GDPR request
It follows that:
\[ C = \{\small{StartRegistration},\small{ConfirmAccount},\small{ResendConfirmation},\small{FulfillGDPRRequest}\} \]
Designing the States
Remember that we have a principle that should always be on our mind when designing State:
The states should consist of the smallest amount of information that together with the knowledge of the input can determine the output.
Our goal is to find the minimum required amount of information to enable suitable reactions. Here less is always more.
This example is not focusing on managing data, but it is possible to define properties on states — this will not have an effect on the general formulas.
Potential customer
This is our initial state \(PotentialCustomer \in S_0\). Any unregistered customer is a potential!
Requires confirmation
- Active
Deleted
This is a final state \(Deleted \in F\)
It follows that:
\[ S = \{ \small{PotentialCustomer}, \small{RequiresConfirmation}, \small{Active}, \small{Deleted} \} \]
and
$$ S_0 = \{\\ \small{PotentialCustomer} \} $$
and
$$ F = \{\\ \small{Deleted} \} $$
How should we react?
The last thing we need is to define our Behavior (δ) and Event (ω) functions.
δ : S x C → S = {
(PotentialCustomer, StartRegistration) → RequiresConfirmation,
(RequiresConfirmation, ResendConfirmation) → RequiresConfirmation,
(RequiresConfirmation, ConfirmAccount) → Confirmed,
(Active, FulfillGDPRRequest) → Deleted,
(RequiresConfirmation, FulfillGDPRRequest) → Deleted
}
and
ω : S x C → E = {
(PotentialCustomer, StartRegistration) → ConfirmationSent,
(RequiresConfirmation, ResendConfirmation) → ConfirmationResent,
(RequiresConfirmation, ConfirmAccount) → AccountConfirmed,
(Active, FulfillGDPRRequest) → AccountDeleted,
(RequiresConfirmation, FulfillGDPRRequest) → ϵ,
}
The ϵ here is special. It says that there is no output for this specific Command-State pair. We will learn more about ϵ and ways we can model handling errors in the next post of this series.
Construction of our Transducer Aggregate!
Now we can finally construct our User Registration Aggregate (or rather non-deterministic Finite-State Transducer) as:
\[ T = \Big(S, C, E, \delta, \omega, \{PotentialCustomer\}, \{Deleted\} \Big) \]
and send the following Commands to it:
$$ C = \{\small{StartRegistration},\small{ResendConfirmation},\small{ConfirmAccount},\small{FulfillGDPRRequest}\} $$
In response we will receive the following Events:
$$ E = \{\small{ConfirmationSent},\small{ConfirmationResent},\small{AccountConfirmed},\small{AccountDeleted}\} $$
Exercise
Given the following commands:
$$ C = \{\small{StartRegistration},\small{ResendConfirmation},\small{FulfillGDPRRequest}\} $$
- Which sequence of events would we get?
- Which state is produced?
Conclusions
- We have learned that process-oriented, temporal models are a great match when dealing with the behaviors of complex systems — and how collaborative modelling techniques have shaped our understanding of these systems.
- We looked into the past of computing advances to rediscover automata theory as a means to model processes, explored different types of machines (FSA, DFA, NDFA, FST) and mapped these to desired properties of temporal Aggregate design.
- We put the math to action and designed a an User Registration Aggregate as a concrete example.
What’s next?
In the next post of the series we will cover the following topics:
- Learning about Accpetors and Sequencers
- Exploring generic operations on FSAs like unions, concatenations and projections.
- Using these operations to naturally transform our current User Registration example into an event-sourced model.
Personal note
These posts are a try to summarize my personal thoughts about this topic for quite some time. I encourage everyone to challenge me on these ideas, and I am the last one to claim that this is the right way to think about these problems.
The hope I have is that readers have fun following me through my thinking process!
Thank you.
This article was originally published on Medium, but unfortunately I don't want to support or use Medium as a publishing platform. Hence I am moving my blog posts to hashnode. The original article can be found here.
